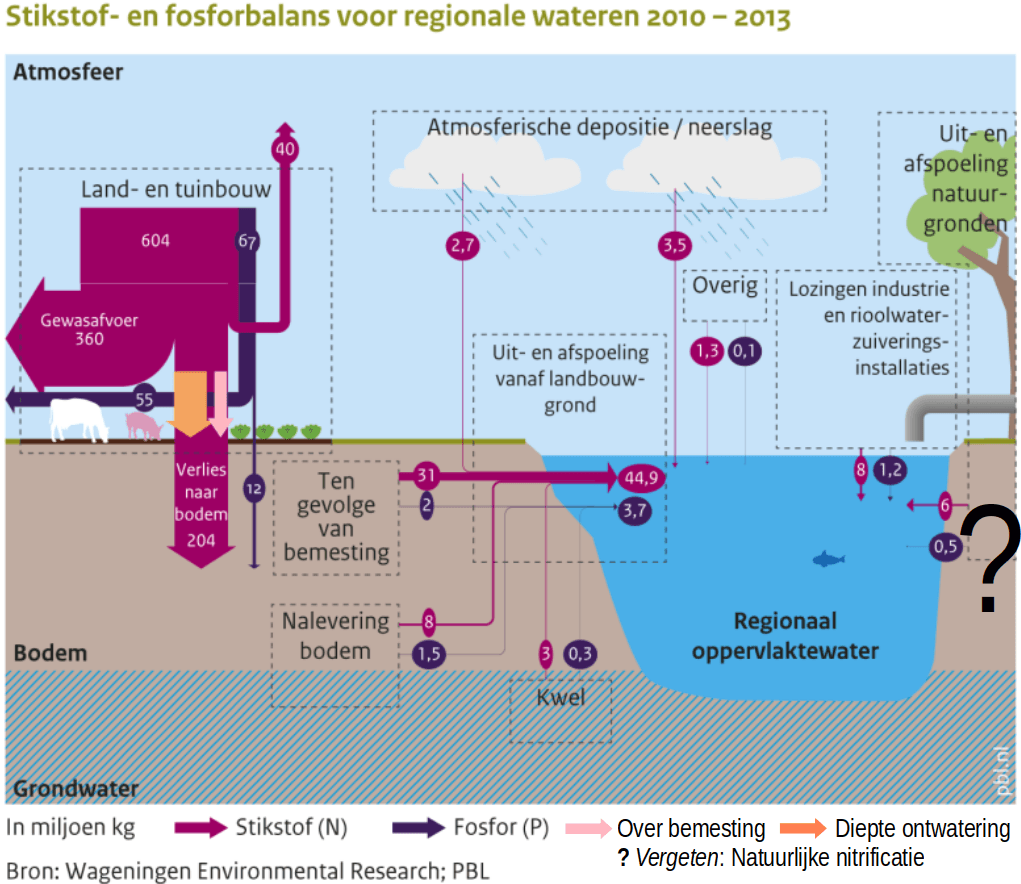
Er gaat te veel mest verloren

De gemiddelde mest verliezen naar de bodem zijn in Nederland met 34% véél te groot.

Bewijs assimilatie doel

   (assimilatie predicaat &
     bemesting voorwaarde &

     natuurlijke nitrificatie voorwaarde &

     depositie voorwaarde )

Het assimilatie predicaat wordt niet voldaan

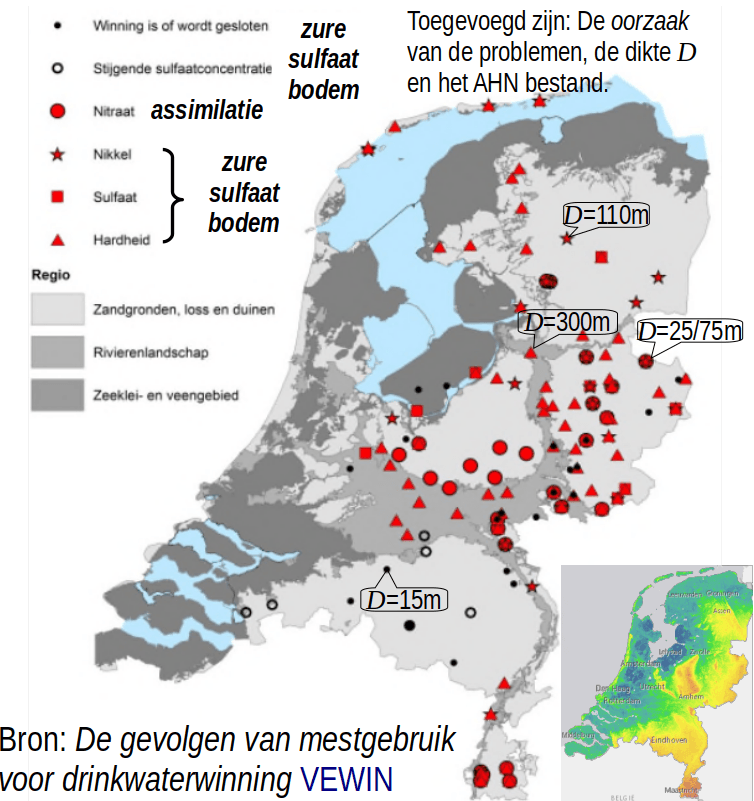
Door diepte ontwatering verwelken de gewassen en ontstaan er mest verliezen naar de bodem die gemiddeld 34% groot zijn en 95% in een bijzonder geval als gevolg van de te lage grondwaterspiegel ten opzichte van het maaiveld.

Daardoor gaat de omzetting van CO2 naar O2 met hetzelfde percentage achteruit waardoor de aarde onnodig opwarmt doordat de koolstofkringloop veel minder effectief is, een deel van de gewasverdamping uitvalt, en er meer natuurbranden zullen ontstaan. De achtergrondverlaging, lokt de drinkwatersector een doodlopende steegje in, waardoor schadevrije winvelden uit beeld zijn, met als gevolg dat er geen oplossing meer is voor het mest probleem.

Grote overeenkomsten

Vaak is de stofwisseling en/of de wortellengte van gelijk ordegrootte, waardoor de assimilatie curve in landbouw en natuurgebieden grote overeenkomsten kent. Grote voorzichtigheid is echter geboden in de omgeving van het interval van verwelking. Bovendien moet ook het dynamische gedrag van de watervoerende laag (golfvoortplanting) kloppen met de praktijk.

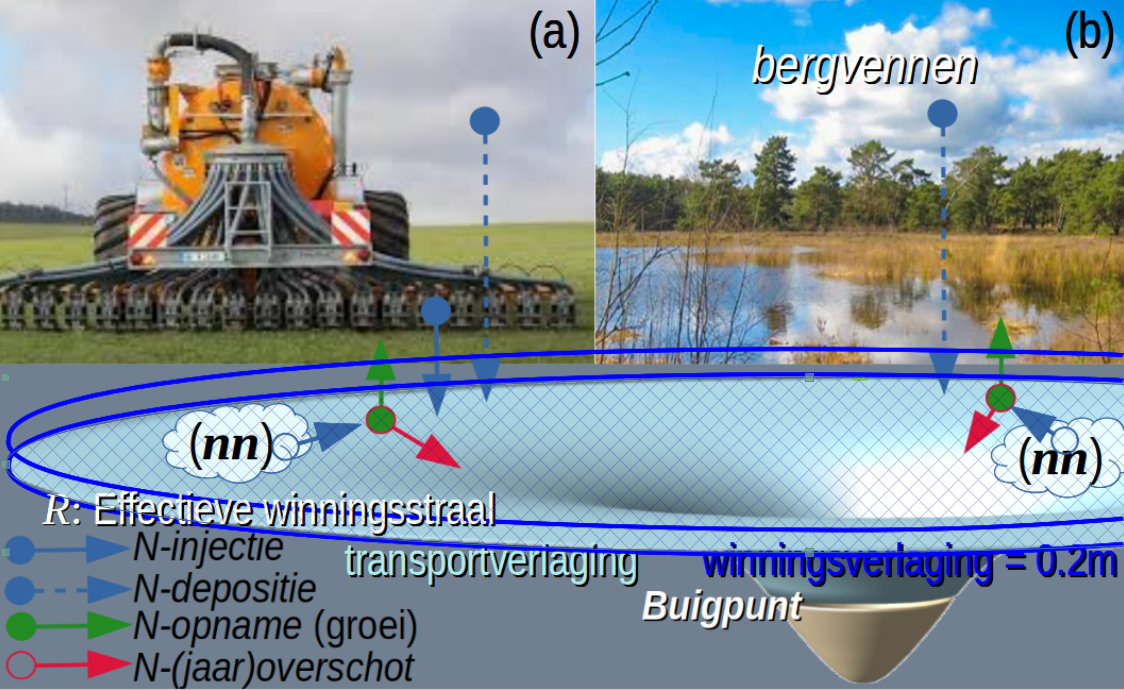
Waterwinning in landbouw en natuur gebieden

In beide gevallen is er ook sprake van natuurlijke nitrificatie waarbij bodembacteriën mest (NH4, NO2^- en NO3^-) maken uit bodemlucht (N2 en O2). Die mest kan niet worden opgenomen door assimilatie bij gebruik van grootschalige winvelden.

Oneigenlijke som

De verlaging van het winveld is de oneigenlijke som van de winningsverlaging (0.2m) en de (optionele) transportverlaging, die vaak (2m...4m) is.

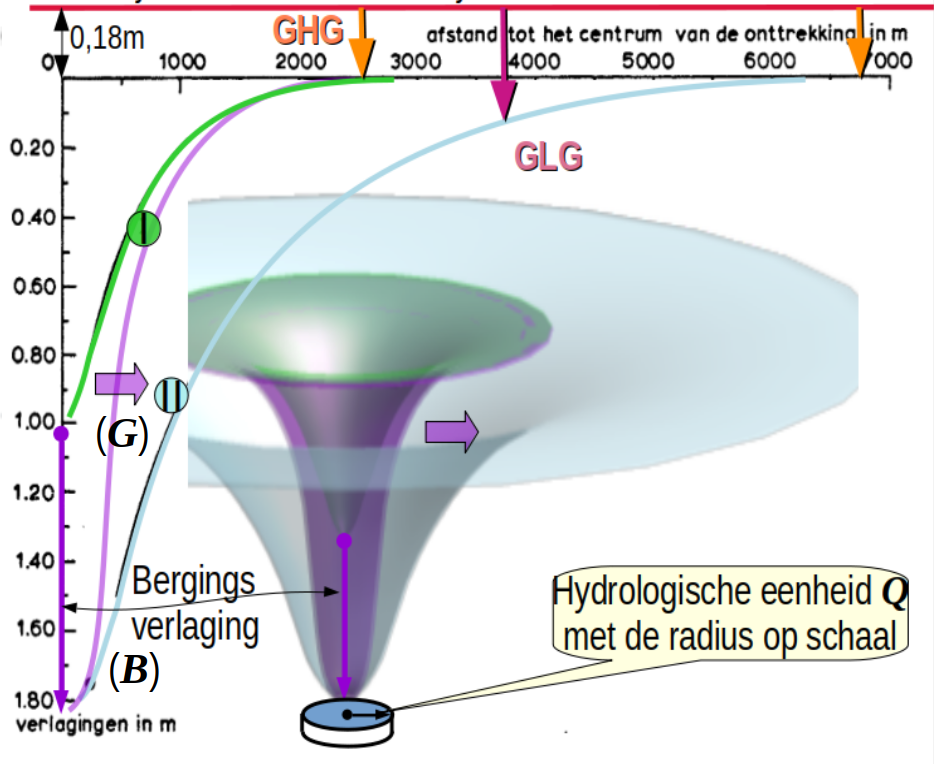
Schaal effect

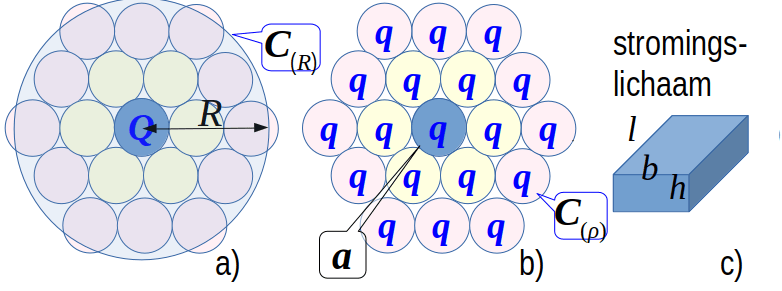
Het debiet Q(t) wordt in het stationaire geval gewonnen uit het gehele winveld A met effectieve winningsstraal R. Maar bij een onbalans tussen vraag een aanbod, komt het gewonnen water uit een kleine cilinder C(ρ) met areaal a en straal ρ ≈ 3D, met D de dikte van de watervoerende laag. De watervoerende laag gedraagt zich op een grote schaal als een halfgeleider. Naast de operatoren (+,-,*,δ) die we gebruiken om differentiaal vergelijkingen te beschrijven, hebben we nu ook rekening te houden met de (<) operator die de gebruikelijke oplossingstechnieken van de vergelijkingen doorbreekt, en de schaal parameter ρ die versterking mogelijk maakt, terwijl de grondwaterstroming niet zomaar vaste stroombanen volgt.

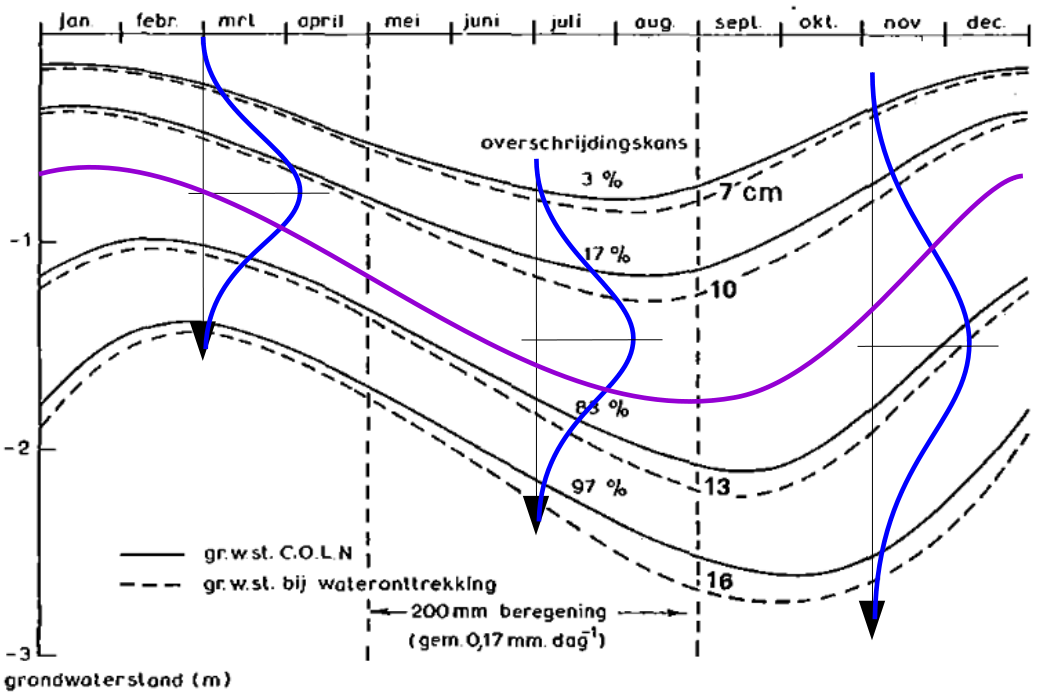
Een foutje is snel gemaakt

Agrohydrologen nemen aan dat je met de {GHG, GLG, GVG} de grondwaterspiegel ten opzichte van het maaiveld hmv(x,y,t) goed kunt beschrijven. Die aanname blijkt vals. Doordat de Laplace voorwaarden niet geldig zijn, ontstaat er rond het maximum van de curve waarop de GHG ligt, een snelle neerwaartse overgang naar de curve waarop de GLG ligt. De teruggaande overgang wordt gemaakt in het rustseizoen. Daardoor is de schade die elk jaar optreedt groter dan op grond van het getoonde grondwaterstandsverloop wordt verwacht.

Twee foutjes ook

Bij hand metingen van de grondwaterspiegel hmv(x,y,t) = h(x,y,t)-mv(x,y), gebaseerd op het gebruik van een grondboor is de winningsverlaging een logisch onderdeel van de {GHG, GLG, GVG}, waarden die de grondwaterstand beschrijven. Als we de grondwaterspiegel berekenen op basis van de transportverlaging, dan wordt er juist geen rekening gehouden met de winningsverlaging. We noemen het verschil c, en tellen deze waarde vervolgens op bij alle GxG waarden. Welke fout wordt er dan gemaakt?

Vervolgens gaan we de schade berekenen met een lineaire interpolatie op de lijn met eindpunten {g.ll, 100%}: en {g.l, 0%} dit geeft: S(hmv + c)=(g.l - (hmv + c))/(g.l - g.ll).

Voor c=0 is dit de werkelijke schade Swerkelijk, maar voor c=0.2m en (g.l - g.ll) = 0.25m geldt: Sberekend=max (0, Swerkelijk-80%). Dit is het doodlopende steegje, waardoor schadevrije winvelden uit beeld zijn.

Schadevrij winveld

Wie de Laplace voorwaarden gebruikt, neemt aan dat de watervoerende laag lineair, plaats (x,y) en tijd (t) invariant, en stabiel is. Die aanname is vals voor het grootschalige winveld in a). Het schadevrije winveld in b) realiseert met een over A gespreide winning, voor alle (x,y) een stationaire verlaging van 0.2m. Daarbij verdwijnt de (optionele) transportverlaging.

Puntspreidfunctie en golfvoortplanting

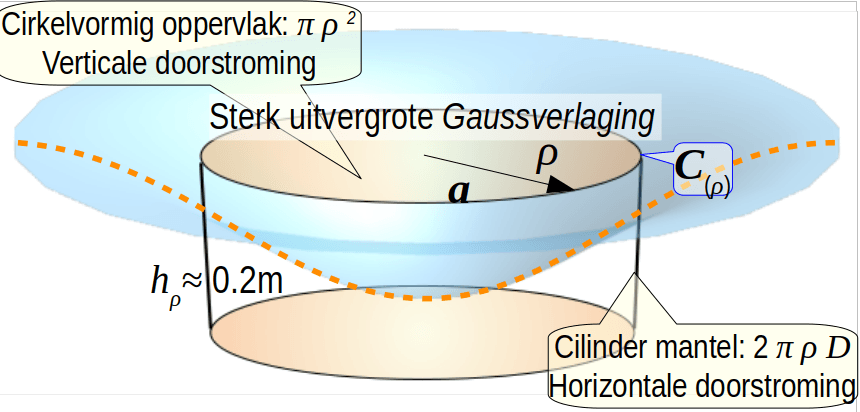
De cilinder C(ρ) is, na correctie op de weerstand van de scheidende lagen in de watervoerende laag zo gekozen dat de weerstand voor een 'verticale' doorstroming van dezelfde orde grootte is als de weerstand voor een 'horizontale' doorstroming. Bij grootschalige winvelden wordt de onbalans in de watervraag en het wateraanbod uit neerslag, met een factor A/a versterkt, waardoor er vanuit de rand van de kleine cilinder C(ρ) een golfvoortplanting ontstaat naar de rand van de cilinder C(R), die door de transportverlaging (I) en (II) in amplitude wordt begrensd. Zo'n golfvoortplanting treedt niet op bij schadevrije winvelden.

Mest verlies 95%

De drinkwatersector wil vanwege het gemak, graag grootschalige winvelden gebruiken, maar omdat de watervoerende laag in verhouding tot de overige afmetingen, héél dun is, ontstaan er door de zeer grote versterkingsfactor A/a ≈ 21, zéér grote problemen doordat uitgerekend aan het begin van het teeltseizoen opeens het assimilatie predicaat niet meer voldaan wordt, door de golf die vanuit de pompput vertrekt richting de effectieve winningsstraal die het winveld begrensd, en op het eind van het teeltseizoen terugkeert.

Niemand die het ziet

De golf zal in veel gevallen de effectieve winningsstraal R niet bereiken, omdat het vaak tot 5 jaar duurt om een transporttrechter te vormen. Maar de golfvoortplanting gaat wel erg snel waardoor in een groot deel, denk aan de helft van het winveld, mest verliezen ontstaan die kunnen oplopen tot 95% van de mestgift, als getoond in de standplaatsvergelijking, waar je ver over de mais kunt kijken.

Om het existentiële probleem op te kunnen lossen moeten de natuurgebieden in een staat gebracht worden die ze vroeger ook konden bereiken, maar nu niet meer. Merk op dat deze wiskundige randvoorwaarde, cruciaal is om de realiseerbaarheid van de doelen aan te kunnen tonen.

Het probleem van verwelking speelt overal in de gematigde klimaat zone, en de effecten zijn in de subtropen zelfs zo groot dat landouw daar nagenoeg onmogelijk is, terwijl boomgroei in een enkele oase voorkomt. Met de verwelking van de gewassen neemt ook de omzetting van CO2 naar O2 flink af, waardoor het klimaatprobleem snel groter wordt. Maar de grens tussen de subtropen en de gematigde zone schuift steeds meer naar het noorden op als gevolg van winning van water met behulp van zeer schadelijke winvelden. Daarom is het van groot belang dat iedereen in Europa begrijpt dat haast geboden is om op mondiale schaal schadevrije winvelden uit te rollen, zeker gelet op de verwachte baby boom in Afrika en de effecten op de natuur en het klimaat die ontstaan doordat de wetenschap in een doodlopend steegje terecht is gekomen.