Convergentie bij sterk niet lineaire algoritmes
Niet lineariteit en het natuurdoel
De grondwaterspiegel h(x,y,t) is bij goede benadering op een kleine schaal een potentiaalveld, maar de assimilatie curve is een sterk niet lineaire functie met de diepte ontwatering d(x,y,t), die gelijk is aan de grondwaterspiegel h(x,y,t) gemeten ten opzichte van het maaiveld in plaats van NAP. De schaal ρ van een dunne watervoerende laag is de straal van een cilinder C(ρ) met een verticale as, waarvoor geldt dat de weerstand voor een verticale doorstroming vanaf het filter van de pompput, gelijk is aan de weerstand voor een horizontale doorstroming van de watervoerende laag. Grootschalige winvelden met een enkele pompput opgesteld dicht bij het zuiveringsstation, kunnen bij een onbalans tussen het actuele debiet Q(t) en de actuele neerslag N(t), snel een relatief klein debiet N(t)a leveren met een verticale stroming uit een klein areaal a rond de pompput, en een relatief groot debiet N(t)A leveren met een horizontale stroming uit een veel groter areaal A. Dit heeft als effect dat snelle effecten met een factor A/a versterkt worden.
De niet-lineaire effecten die ik hier beschrijf liggen in twee verschillende vakgebieden die door de specialisatie in het onderzoek en het onderwijs, ook in verschillende onderzoeksgroepen bestudeerd worden. Als we willen dat het natuur doel gerealiseerd wordt, is het van groot belang dat het beide delen van het niet-lineaire gedrag zonder fouten te maken, het onderwerp van studie zijn.
Door een Constructief Bewijs te maken lukt het om synthese techniek te gebruiken om de fysisch chemische eigenschappen, met voorschriften en predicaten, en een correct werkend monitoring programma, te scheiden van het ontwerp van het best mogelijke schaalbare winveld, dat wel geschikt is om het natuur doel te realiseren.
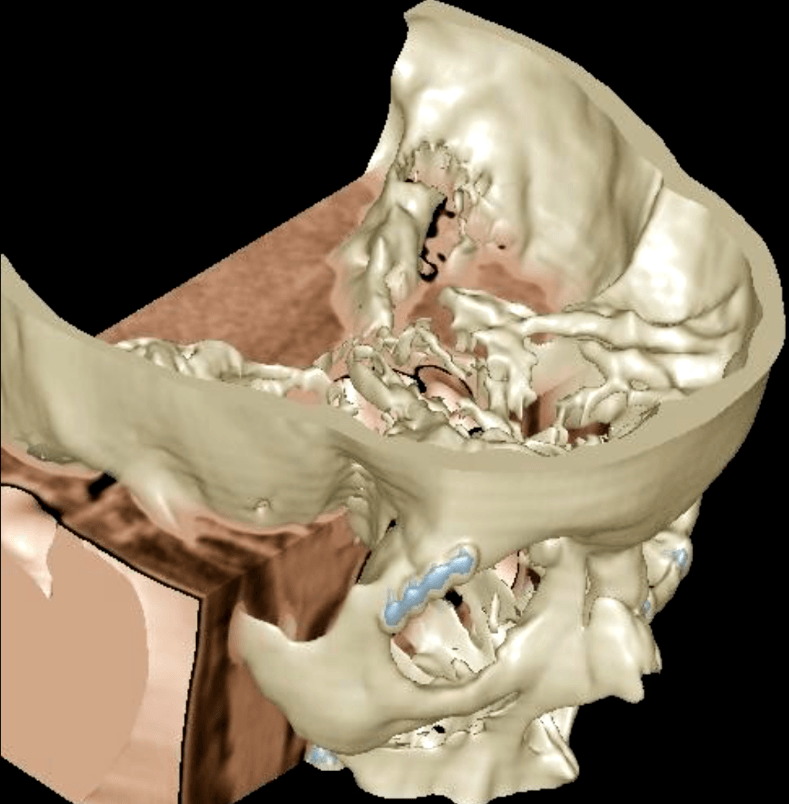
De convergente insluiting
Als je het verschil ziet tussen de beeldvorming met de oude volume visualisatie technieken, en de door onze onderzoeksgroep ontwikkelde techniek gebaseerd op een convergente insluiting, dan zie je in een oogopslag waarom de convergente insluiting zo belangrijk is.
Met een scanner kan een 3D afbeelding gemaakt worden van materialen met elk een eigen dichtheid voor een CT-, MRI-, PET-, opname etc.. De dichtheidswaarde wordt voor alle opname technieken de grijswaarde genoemd. De scanner heeft voor stationaire afbeeldingen een 3D puntspreidfunctie h(x,y,z) en voor dynamische opnamen, bijvoorbeeld van een kloppend hart, een 4D puntspreidfunctie, h(x,y,z,t). Die laatste categorie is belangrijk omdat zwakke plekken en ook verstoppingen in bloedvaten herkend kunnen worden aan de dynamiek van de vaatwand.
Ik ga nu nog uitsluitend verder met het stationaire geval. Een punt in de grijswaarde ruimte heeft effect op alle 8 omringende punten van het grijswaardenveld g(x,y,z). Daardoor zijn we nu in staat om voor alle (x,y,z) het grijswaarden veld te reconstrueren uit de grijswaarden van de 8 omringende punten met behulp van een (tri-lineaire) interpolator als gtri(x,y,z).
Voor de reconstructie van de schedel en het hoofd, moeten we op de zichtstraal de grijswaarde bepalen giso die halverwege de grijswaarde van zacht weefsel en de grijswaarde van bot ligt.
Het maakt voor de kwaliteit van de visualisatie van het 3D object en de daarbij horende beeldkwaliteit enorm veel verschil of we de toepassing van de 50% drempelwaarden en de bepaling van de kleurnuance RGBα toepassen op alle 8 omringende punten, en daarna met behulp van een tri-lineaire interpolator uit de 8 omringende punten de RGBα waarde bepalen op een sample locatie op de zichtstraal uit de 8 RGBα waarden, of dat we eerst de drempelwaarde gebruiken om het iso-oppervlak te bepalen door een convergente insluiting, als getoond, om pas op het oppervlak de kleurnuance RGBα te bepalen met behulp van de oppervlakte normaal. Dit heeft te maken met het feit dat de tri lineaire interpolator die we gebruiken om het veld dat vastligt door de 8 omringende punten lineair is in (x), (y) en (z) maar van de graad 3 is in (x,y,z). De regula falsi formule, die zeer snel convergeert, maakt gebruik van tenminste 1 waarde boven de gezochte grijswaarde en tenminste 1 eronder, en berekent het gezochte nulpunt met een rechte lijn benadering. Vaak geeft dit weer een punt boven de gezochte iso-grijswaarde en een eronder, maar het kan ook voorkomen dat we nog slechts waarden aan een zijde van de gezochte grijswaarde vinden. Dan zitten we op een zichtstraal die het grijswaarden oppervlak niet raakt, maar erlangs scheert, wat impliceert dat we nog niets weten over de kleur en de kleurnuance die afhangt van de oppervlakte normaal. Wat we hier leren is dat de bepaling van de kleurnuance en de tri-lineaire interpolatie niet in een andere volgorde uitgevoerd mogen worden.
Operaties met een niet lineariteit mogen uitsluitend in de oorspronkelijke volgorde uitgevoerd worden.



