Realisatie van de winvelden

Het neerslag budget

Een winveld wordt gespreid gevoed met neerslag N(t) en levert het debiet Q(t) dat afhangt van de actuele vraag naar grondwater. Het drinkwaternetwerk buffert een minimale hoeveelheid drinkwater, in een watertoren, of een modernere hydrofoorinstallatie. Het jaargemiddelde van de neerslag N bedraagt in Nederland 0.8m. Variaties in de neerslag hoeveelheid worden doorvertaald naar variaties in de aanwas van de grondwaterspiegel. Daarbij treedt in verband met de korrels in de bodem een versterking, groot 1/μ ≈ 3 op, met μ de porositeit. Het is een goed gebruik om {assimilatie, winning, surplus} een gelijke toedeling te kiezen, waarbij het surplus voor horizontaal bestaat uit kwel die via de lokale watergangen afgevoerd wordt, en voor hellend zich voegt het surplus zich bij een onderstroom die een aantal schaal eenheden (cilinders) later uittreedt. Voor het droge jaar 2017 geeft deze versterkingsfactor een gemiddelde aanwas van de grondwaterspiegel groot {0.8m, 0.8m, 0.2m}, hetgeen impliceert dat er gemiddeld nog steeds een surplus van 0.2m van 0.8m overblijft van de nominale grondwateraanwas. Wie wil dat het winveld alle mest door assimilatie overdraagt aan de groei van het gewas, moet ervoor zorgen dat de grondwaterspiegel zich beweegt in het interval van volledige assimilatie, daarom mag de assimilatie term nooit kleiner worden dan, 1 hetgeen bij de gemiddelde neerslag een aanwas geeft van 0.8m. Met behulp van deze regel wordt de toewijzing uit het neerslag budget:

Nbudget = N(α)(t) {1 , α , (2 – α)} / 3.

Voor α = 0 beschrijft dit de nul-toestand, α = 1 beschrijft de situatie bij winning, α < 1 is een voldoende voorwaarde die zeker stelt dat de onderstroom op peil blijft, α < 2 is een voldoende voorwaarde (de synthese kan verder, maar wel binnen beperkende voorwaarden), terwijl 2 < α is een noodzakelijke voorwaarde (door de overschrijding kunnen de doelen überhaupt niet gerealiseerd worden).

Om de doelen te kunnen realiseren voor grootschalige winvelden voor horizontaal, gebruik ik de eliminatie van de transportverlaging en voor hellend de techniek van winning door infiltratie. Bij beide realisatie vormen speelt de diepte ontwatering die het mogelijk maakt om een maximale assimilatie te realiseren de hoofdrol. Met het neerslag budget kun je tijdens de synthese, door de waarde van α aan te passen, de diepte ontwatering bijstellen, om te voorkomen dat de assimilatie aangetast wordt.

De grondwaterspiegel was horizontaal

Ik zal binnen het vakgebied der hydrologie de grondwaterstand h(x,y) voor alle (x,y) en (t) met de logica benaderen. Dit heeft als voordeel dat ik niet hoef te beginnen met een differentiaalvergelijking die voldoet aan de Laplace voorwaarden, met als gevolg dat we zouden moeten veronderstellen dat de voedende neerslag N en het debiet Q dat de vorm van de grondwaterspiegel beïnvloedt nog slechts een constante waarde aan zou mogen nemen, terwijl het op voorhand al duidelijk is dat het grondwater de weg van de minste weerstand zal volgen. De actuele waarde van de verticale stromingsweerstand is, gegeven de dikte D van de dunne watervoerende lagen die we beschouwen, in verhouding zo klein dat deze niet ter zake doet bij de berekening van de grondwaterstand h(x,y). Bij een grootschalig winveld is de gereduceerde grondwateraanvulling binnen de effectieve winningsstraal R van veel groter belang in verband met het proces van autonome herverdeling van grondwater dat ontstaat bij een gespreide winning van het grondwater.

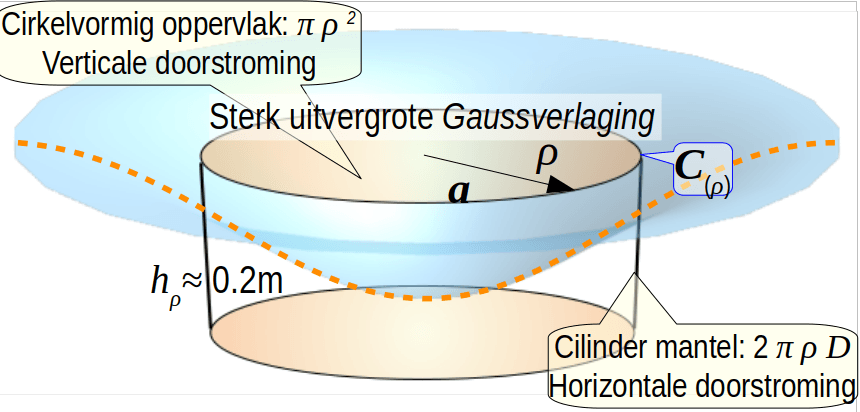
De weerstand van een stromingslichaam is evenredig met z'n lengte en omgekeerd evenredig met het doorstroomde oppervlak. Voor een cilinder C(ρ) is het verticaal doorstroomde oppervlak π ρ2 en het radiaal & horizontaal doorstroomde oppervlak van de cilindermantel is: 2 π ρ D. Gelijkstellen van de doorstroomde oppervlakken geeft π ρ2 = 2 π ρ D, dit geeft: ρ = 2 D.

Binnen de cilinder C(2D) neemt de horizontale weerstand voor een radiale doorstroming voor r→0 met 1/r, zeer snel toe, waardoor er binnen deze cilinder altijd een overwegend verticale stroming zal zijn, daarom willen we dat daarbuiten de doorstroomde lengte ook gelijk is. Daarom is: ρ  ≈ 3 D een geschikte waarde voor de eenheidsstraal ρ van de cilinder C(3D) die ik voortaan met C(ρ) zal aanduiden. Deze cilinder maakt het, in een dunne watervoerende laag, mogelijk om met een, in eerste aanleg, zuiver verticale stroming grondwater te winnen met een minimaal aantal pompputten. Merk op dat zo'n berekening ook uitgevoerd kan worden voor een dunne watervoerende laag die bestaat uit meerdere horizontale lagen met elk een eigen specifiek geleidingsvermogen k.

De eliminatie van de transportverlaging

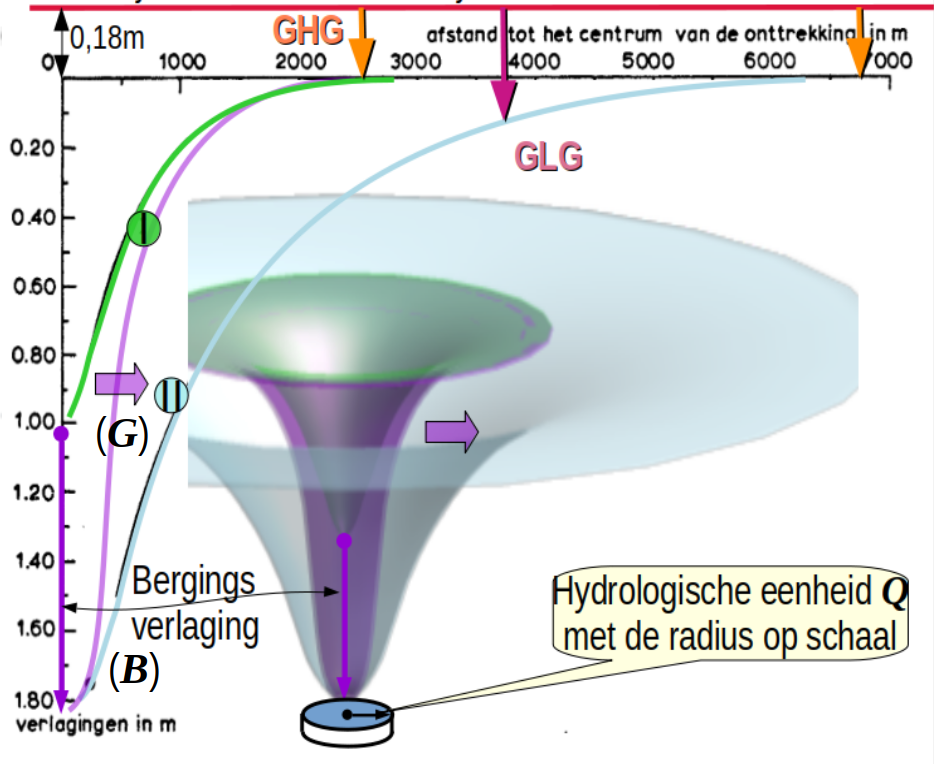
We hebben nu de schaal parameter ρ van de watervoerende laag bepaald, die prof. J.J. de Vries al aankaartte tijdens de najaarsbijeenkomst van de NHV over de achtergrondverlaging en ook de eerste stappen gezet, nodig om een gespreid winveld b) te (kunnen) maken, met een verlaging van ~0.2m door de eliminatie van de transportverlaging die in een klassiek winveld a) heel prominent aanwezig is.

De transportformule van Dupuit

De stationaire transportformule van Dupuit kan afgeleid worden door voor alle stralen (r) tussen {ρ, R} het potentiaalverschil te berekenen over een cilindermantel met dikte δr als gevolg van een zuiver horizontale doorstroming, die voor alle (z), in het (x,y) vlak dezelfde doorstroming realiseert, voor het stationaire debiet Q. De integraal telt voor elke r het bijbehorende potentiaal verschil over de weerstandswaarde van de cilindermantel met dikte δr op.

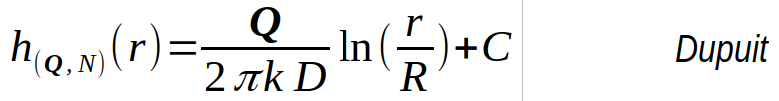
Er wordt aangenomen dat de dikte D overal even groot is. Bij dunne watervoerende lagen, gekarakteriseerd door h << √A zijn die aannames, als er gelijktijdig grote debieten Q worden gewonnen, om vele redenen vals. Eén daarvan is dat een homogene laag met dikte D=10m, van de watervoerende laag, rond de pompput wel 2 tot 4m dunner kan worden als gevolg van de som van de transportverlaging en de winningsverlaging. Het is belangrijk om nauwkeurig te werken, want als je een deel van de verlaging verklaart uit de winningsverlaging heeft dat veelal een groot effect op de berekende schade van een winning, waardoor er ongevraagd een problematisch winveld ontstaat, waar veel mest uitspoelt en ook zure sulfaatbodems kunnen ontstaan. Alle doelstellingen zijn dan niet meer realiseerbaar.

De complementaire analyse

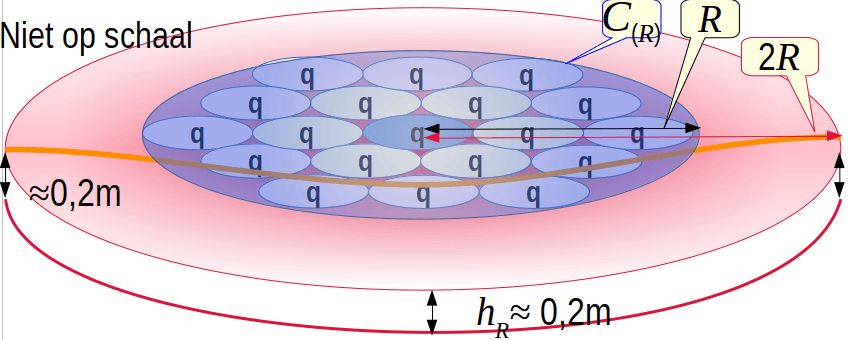
Voor het horizontale transport van het grondwater was de transportformule van Dupuit favoriet, maar zeker niet adequaat. Toepassing van de effectieve winningsstraal R laat zien dat er met een gespreid winveld b), voor alle r < R uit de cilinder C(R) met een zuiver verticale stroming het debiet Qwinbaar = π R2 Nwinbaar wordt gewonnen. Maar in de formule van Dupuit, komt helemaal geen neerslag N voor en ook geen stroming langs de z-as. Het gehele debiet Qwinbaar wordt conceptueel door de mantel van de cilinder C(R) aangevoerd vanuit het oneindige. Na autonome herverdeling van grondwater blijkt voor het gespreide winveld dat ¼ van de neerslag uit de effectieve winningsstraal R komt en ¾ uit een straal 2R. Hiermee hebben we genoeg informatie om de stationaire stromingsvector (x,y,z) binnen de cilinder C(2R) nauwkeurig te berekenen.

Met deze resultaten zien we nu ook dat de totale verlaging van de puntwinning de waarde continue som is van de transportverlaging en de winningsverlaging.

De gespreide puntwinning

Bij winning van een groot debiet Q=A/a q kan dit via een verticale stroming gespreid gewonnen worden met A/a pompputten die elk een debiet q winnen uit een areaal a als in b) vanuit een cilinder C(R) met R de effectieve winningsstraal. Als de stroming volledig stationair is, vinden we ook een volledig stationaire oplossing. Maar als er een onbalans is tussen N (t) en Q (t), dan zal een zuivere puntwinning de onbalans met een factor A/a versterken. Bij de gespreide puntwinning, die geen gebruik maakt van transport van grondwater door de watervoerende laag is die versterking a/a = 1.

Autonome herverdeling van grondwater

Het is nuttig om kennis te nemen van de theorie van de herverdeling van grondwater, beschreven op pag. 857 e.v. van het boek, van de gerenommeerde Nederlandse hydroloog 1dr. G.A. Bruggeman, die bij het RID/RIVM werkzaam was. Ditzelfde effect treedt óók op bij de herverdeling van gassen, beschreven in de divergentie stelling van Gauss.

De divergentie stelling is ook bekend van de statistiek van de grote aantallen.

De uiteindelijke vorm van de grondwaterspiegel wordt, bij een cilindrische verlaging hρ = ¼ x 0.8m gegeven door een oneindig herhaalde toepassing van het principe van herverdeling van grondwater, dat heel netjes wordt benoemd met de term convolutie, hetgeen in normaal Nederlands afwikkeling betekent, als in de eerste figuur.

Autonome herverdeling van grondwater op een snijvlak bij een lijnwinning
Met dit gespreide winveld met een winningsverlaging van 0.2m spoelt er geen mest meer uit
De dynamiek van de zuivere puntwinning versterkt de onbalans tussen de neerslag en het debiet met A/a

Dit is in dit geval een (autocorrelatie) proces waarbij a) overgaat in de roze driehoekvorm in b) terwijl deze curve, bij een 2e convolutie stap, ook weer overgaat in de c3 continue gladde oranje curve die is opgebouwd uit polynoom segmenten met een graad <= 3. Kenmerkend bij herverdeling is dat bij een verticale snede uit een lijnwinning langs de stroomlijnen, het oppervlak beneden de grondwaterspiegel in het snijvlak constant blijft. Er zijn subtiele verschillen in de vorm van de puntspreidfuncties. De puntspreidfunctie van een puntwinning met een klein debiet q, zoals de elementaire Gaussverlaging, kan worden beschreven met polaire coördinaten: h(r,φ) waarbij (r,φ) voor alle 0 ≤ φ < 2 π, een 2D plaats coördinaat is. In dat geval kunnen we de rechthoek die we gebruikt hebben bij het proces van autocorrelatie vervangen door een tweetal driehoeken met een waarde π, voor r={-ρ,+ρ} en een waarde 0 voor r=0. Omdat we het resultaat altijd gaan benaderen door de best mogelijke polynoom approximatie, zal ik aan de subtiele verschillen die daarbij optreden verder geen aandacht besteden. Onder de grondwaterspiegel is de waterbalansanalyse toe te passen. Daarmee volgen we de methode die ir G.W. Bloemen en ir. W.C. Visser, met eenvoudige middelen hebben verkend aan de landbouwhogeschool. Het toepassen van convolutie veronderstelt dat de Laplace voorwaarden geldig zijn. Aan die voorwaarde is bij de gespreide puntwinning voor horizontaal, gegeven de opdeling van de neerslag N(α), en het gebruik van kleine debieten q, voor het stationaire geval altijd voldaan. Maar als we naar grotere debieten Q overgaan, dan moeten we de winning van het grondwater beschrijven met een gespreid winveld. In dat geval is er geen transport grondwater door de watervoerende laag, het hele debiet Q gaat door een stelsel van buizen, buiten de watervoerende laag om, naar het zuiveringsstation.

Bij een zuivere puntwinning onder stationaire omstandigheden, moeten zowel de effecten van de winning en van het transport binnen een straal 2R beschouwd worden. Hiervoor moeten we met de winningsverlaging van het gespreide winveld rekenen en met de aangepaste transportverlaging van Dupuit. Voor het niet stationaire geval zijn geen eenvoudige analyse methoden mogelijk. Dit is een directe consequentie van het schaal probleem dat prof. J.J. de Vries heeft benoemd.

In de beschrijving van het onderzoek van G.W. Bloemen, beschrijf ik hoe een onbalans tussen N (t) en Q (t) waarbij Q (t) de overhand neemt, de grondwaterspiegel eerst naar de stationaire oplossing gaat van het nieuwe evenwicht, om vervolgens met een golfbeweging verder te gaan. Deze processen kunnen niet met een 2-tal onttrekkingstrechters van een stationaire onttrekking beschreven worden, maar wel met de animatie van het vlak V(X,T)(x,y,h)(t) op een plaats (x,y) schaal (X) en een tijd (t) schaal (T) met die met de waterbalansanalyse en de schaal transformatie aangestuurd kan worden. Ik zal nog nader ingaan op de achterliggende theorie.

De theorie met de transportverlaging, de winningsverlaging en de bistabiele relaxatie oscillatie is opgebouwd vanuit de complementaire analyse voor horizontaal en het concept dat het grondwater, indien nodig, heel snel de weg van de minste weerstand kan volgen. Deze methode onderscheid zich, door het gebruik van de elementaire Gaussverlaging als basisfunctie, van het onderliggende systeem dat niet aan de Laplace voorwaarden voldoet, maar beschreven kan worden met de waterbalansanalyse en de schaal transformatie om voor alle (x,y) en (t) de grondwaterspiegel te bepalen met behulp van een approximatie algoritme, dat geen aannames doet betreffende de Laplace voorwaarden. Systemen wel die aan de Laplace voorwaarden voldoen, worden normaal beschreven worden met eigenfuncties. bij zijn grondwaterstroombanen te onderscheiden, zoals dat ook het geval is bij de Analytische Elementen Methode. De 3,4AEM beschrijft een gladde grondwaterspiegel, maar er wordt géén gebruik gemaakt van de complementaire analyse, en er wordt ook geen onderscheid gemaakt tussen bijvoorbeeld de transportverlaging en de winningsverlaging.

  1. G.A. Bruggeman, Analytical Solutions of Geohydrological Problems, Elsevier 1999, 956 pages.
  2. G.W. Bloemen, De berekening met een waterbalansmodel van de daling van freatisch grondwater als gevolg van grondwater winning, ICW Nota 758, aug. 1973
  3. H.M. Haitjema, Modeling three-dimensional flow in confined aquifers by superposition of both two- and three-dimensional analytic functions. Water Resour. Res., 21(10):1556-1557
  4. O.D.L. Strack, "Groundwater Mechanics" Prentice Hall, 1989.

Hier plakken